Grundlagen zur Weibull-Verteilung

www.weibull.de

Die von dem Schweden Waloddi Weibull entwickelte Verteilung ist eine universelle Verteilung, mit der die unterschiedlichsten Fragestellungen behandelt werden können. Für Lebensdauer und Zuverlässigkeit ist die Weibull-Verteilung weltweiter Standard. Das sogenannte Weibull-Netz zeigt, wie viele Einheiten in % nach einer Lebensdauer(zeit) t ausgefallen sind, bzw. ausfallen werden.

Übersicht

§ Software für Weibull-Analysen

§ Schulungen für Weibull und Zuverlässigkeitsmethoden

§ Weibull Steckbriefe als PDF

§ Allgemeine Grundlagen

§ Aufbereitung der Daten

§ Das Weibull-Netz

- Bestimmung der Weibull-Parameter

- Interpretation der Ergebnisse

- Allgemeine Probleme bei der Auswertung

- Der Vertrauensbereich

- Bestimmung der Ausfallfreien Zeit to

§ Prüfung auf Mischverteilung

§ Vergleich von 2 Weibull-Verteilungen

§ Berücksichtigung noch nicht eingetretenen Ausfällen- Sudden Death

§ Prognose für noch nicht eingetretene Ausfälle

- Ermittlung der Laufstreckenverteilung aus den Beanstandungen

§ Zuverlässigkeit in Tests mit normaler Belastung

§ Wöhlerdiagramm aus Weibull-Auswertung ableiten

§ Literatur

Software für Weibull-Analysen

Visual-XSel 20.0 ermöglicht schnell und einfach alle wichtigen Analyse-Verfahren. Spezielle Methoden und deutsche Standards nach VDA 3.2 und VDA 3.3 werden unterstützt.

---

Allgemeine Grundlagen

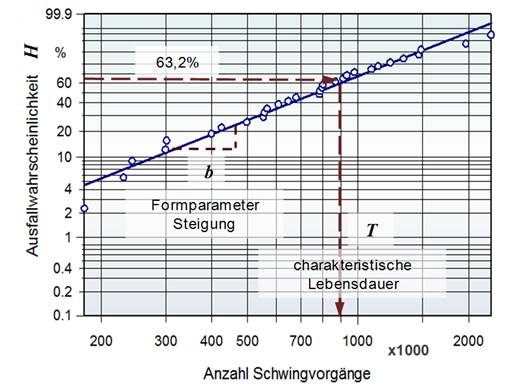
Die Weibullanalyse ist die klassische Zuverlässigkeitsanalyse oder das klassische Lebensdauerdiagramm und hat besonders in der Automobilindustrie eine große Bedeutung. Aus dem sogenannten Weilbull-Netz lassen sich die "Charakteristische Lebensdauer", sowie eine bestimmte "Ausfallwahrscheinlichkeit von bestimmten Bauteilen oder Komponenten ablesen.

Es hat sich als vorteilhaft erwiesen, die Summenverteilung der Ausfälle als Basis anzunehmen. Die Weibull-Verteilung ist eine spezielle Verteilungsform, die für diesen Anwendungsfall besonders geeignet ist. Verallgemeinert handelt es sich bei der Weilbullverteilung um eine Exponentialverteilung. Mit dieser Darstellung wird gearbeitet, weil

 - sehr viele Verteilungsformen mit der Weibull-Verteilung dargestellt werden können,
 - die Weibull-Funktion mathematisch leicht zu handhaben ist,
 - zeitabhängige Ausfallmechanismen als Gerade erscheinen und
 - weil sie sich in der Praxis bewährt hat

Wenn die Ausfallwahrscheinlichkeit im linearen Diagramm dargestellt wird, erhält man eine über den gesamten Verlauf nicht einfach abzulesende S-förmige Linie. Durch Verzerrung des Ordinatenmaßstabes (doppellogarithmisch) und der Abszisse (logarithmisch) wird die S-förmige Linie zu einer Geraden (linearisierte Ausgleichsgerade). Die Weibull-Verteilungsfunktion lautet in der vereinfachten 2-parametrigen Form (siehe /1/ und /2/):

mit

H = Ausfallwahrscheinlichkeit bzw. Ausfallhäufigkeit (normiert auf 1, in % mal 100)

t  = Lebensdauervariable (Fahrstrecke, Einsatzdauer, Lastwechsel usw.)

T =  Charakteristische Lebensdauer, bei der 63.2% der Einheiten ausgefallen sind (für t=T gilt H = 100% (1 - 1/e) = 63.2 % ).

b  = Formparameter, Steigung der Ausgleichsgeraden im Weibull-Netz oder in der 3-parametrigen Form

mit t_o = ausfallfreie Zeit

In den meisten Fällen kann mit  t_o = 0 gerechnet werden, was der 2-parametrigen Form entspricht. Einige Bauteile verhalten sich trotz einer Beanspruchung so, dass erst nach einer Betriebszeit to Ausfälle auftreten. Bei diesem Verhalten liegen die Punkte über dem Lebensdauermerkmal meist nach rechts gekrümmt im Weibull-Netz. Bei der links steil abfallenden Kurve kann man sich mit  t_o  den Schnittpunkt der Kurve mit der Nulllinie vorstellen, die im logarithmischen Maßstab im Unendlichen liegt.

Aufbereiten der Daten

Übersicht, Methoden, Software, Schulungen -> www.crgraph.de